I've always loved this article explaining how to compute a 2D visibility polygon in real time. This can be used for real-time lighting, or computing what can be seen by the player or an AI agent, etc.
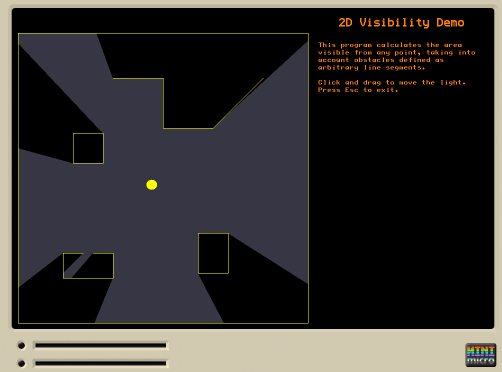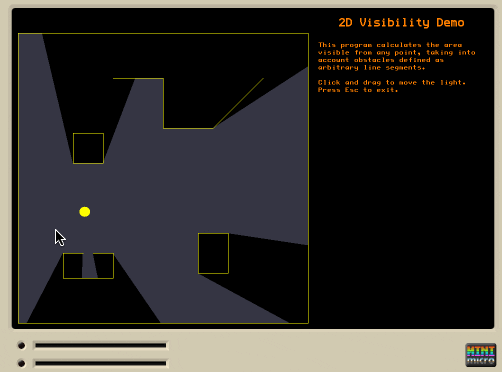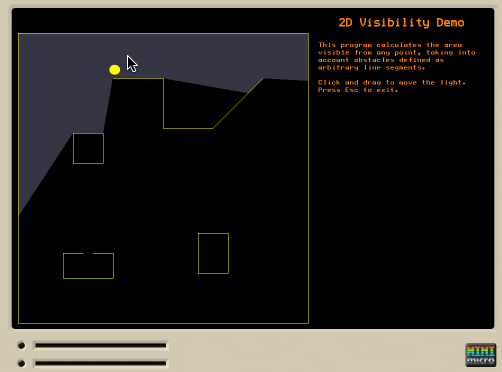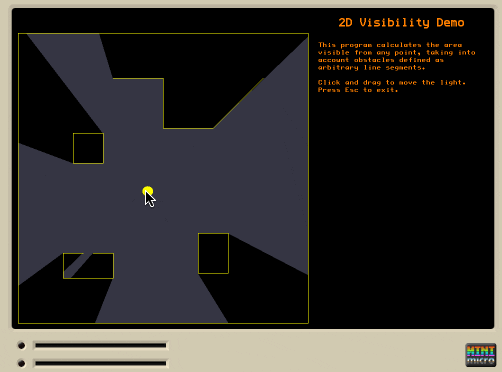
I ported the author's Haxe implementation to MiniScript, more or less directly, except that I changed the code which figures out which of two walls is "in front" relative to the viewpoint. My version first checks if the two walls have a common endpoint (i.e. meet at a corner). If so, then we take whichever one is closer to the user (using a standard distance-to-line-segment function). Otherwise, we check whether both sides of one wall are on the same side of the other wall as the viewpoint (similar to the original code). I found that both these checks were necessary to handle all cases in my testing.
This code will be one of the demos that ships with Mini Micro 0.9, but for posterity, here's the code as it stands today.
// 2D Visibility
//
// port/update of:
// https://www.redblobgames.com/articles/visibility/Visibility.hx
//
// To use in your own projects:
// 1. copy or import this code
// 2. create a new Visibility object
// 3. call loadMap, addBlock, or addSegments as desired
// 4. then, whenever the viewpoint changes:
// a. call setViewpoint
// b. call sweep
// c. do something with the output polygon.
import "mathUtil"
Point = {}
Point.x = 0
Point.y = 0
Point.make = function(x, y)
p = new Point
p.x = x
p.y = y
return p
end function
EndPoint = new Point
EndPoint.begin = false
EndPoint.segment = null
EndPoint.angle = 0
EndPoint.visualize = false
EndPoint.make = function(x, y, segment, visualize)
p = new EndPoint
p.x = x
p.y = y
p.segment = segment
p.visualize = visualize
return p
end function
Segment = {}
Segment.p1 = null // EndPoint
Segment.p2 = null // EndPoint
Segment.d = 0
Segment.make = function(p1, p2)
s = new Segment
s.p1 = p1
s.p2 = p2
return s
end function
Visibility = {}
Visibility.make = function()
v = new Visibility
v.segments = []
v.endpoints = []
v.viewpoint = new Point
v.output = []
v.demo_intersectionsDetected = []
return v
end function
// Helper function to construct segments along the outside perimeter
Visibility.loadEdgeOfMap = function(size, margin)
self.addSegment margin, margin, margin, size-margin
self.addSegment margin, size-margin, size-margin, size-margin
self.addSegment size-margin, size-margin, size-margin, margin
self.addSegment size-margin, margin, margin, margin
end function
// Load the edge of the map, and clear out any previous
// segments and endpoints.
Visibility.loadMap = function(size, margin)
self.segments = []
self.endpoints = []
self.loadEdgeOfMap size, margin
end function
// Add a segment, where the first point shows up in the
// visualization but the second one does not. (Every endpoint is
// part of two segments, but we want to only show them once.)
Visibility.addSegment = function(x1, y1, x2, y2)
segment = new Segment
segment.p1 = EndPoint.make(x1, y1, segment, true)
segment.p2 = EndPoint.make(x2, y2, segment, false)
segment.index = self.segments.len // for debugging!
self.segments.push segment
self.endpoints.push segment.p1
self.endpoints.push segment.p2
end function
// Add a set of segments (walls) defined by a chain of
// [x,y] points.
Visibility.addSegments = function(points)
for i in range(0, points.len-2)
self.addSegment points[i][0], points[i][1], points[i+1][0], points[i+1][1]
end for
end function
Visibility.addBlock = function(x, y, width, height)
if height == null then height = width
self.addSegments [
[x-width/2, y-height/2],
[x-width/2, y+height/2],
[x+width/2, y+height/2],
[x+width/2, y-height/2],
[x-width/2, y-height/2]]
end function
// Set the light location. Segment and EndPoint data can't be
// processed until the light location is known.
Visibility.setViewpoint = function(x, y)
self.viewpoint = Point.make(x, y)
for segment in self.segments
segment.d = mathUtil.distanceToLineSegment(segment.p1, segment.p2, self.viewpoint)
// NOTE: future optimization: we could record the quadrant
// and the y/x or x/y ratio, and sort by (quadrant,
// ratio), instead of calling atan. See
// <https://github.com/mikolalysenko/compare-slope> for a
// library that does this. Alternatively, calculate the
// angles and use bucket sort to get an O(N) sort.
segment.p1.angle = atan(segment.p1.y - y, segment.p1.x - x)
segment.p2.angle = atan(segment.p2.y - y, segment.p2.x - x)
dAngle = segment.p2.angle - segment.p1.angle
if dAngle <= -pi then dAngle = dAngle + 2*pi
if dAngle > pi then dAngle = dAngle - 2*pi
segment.p1.begin = (dAngle > 0)
segment.p2.begin = not segment.p1.begin
end for
end function
// Helper: leftOf(segment, point) returns true if point is "left"
// of segment treated as a vector. Note that this assumes a 2D
// coordinate system in which the Y axis grows downwards, which
// matches common 2D graphics libraries, but is the opposite of
// MiniScript, so I'll need to fix this (ToDo).
Visibility.leftOf = function(s, p)
// This is based on a 3d cross product, but we don't need to
// use z coordinate inputs (they're 0), and we only need the
// sign. If you're annoyed that cross product is only defined
// in 3d, see "outer product" in Geometric Algebra.
// <http://en.wikipedia.org/wiki/Geometric_algebra>
cross = (s.p2.x - s.p1.x) * (p.y - s.p1.y) -
(s.p2.y - s.p1.y) * (p.x - s.p1.x)
// print "cross of " + (s.p2.x - s.p1.x)+","+(s.p2.y - s.p1.y) +
// " and " + (p.x - s.p1.x)+","+(p.y - s.p1.y) + " = " + cross
return cross < 0
// Also note that this is the naive version of the test and
// isn't numerically robust. See
// <https://github.com/mikolalysenko/robust-arithmetic> for a
// demo of how this fails when a point is very close to the
// line.
end function
// Helper: do we know that segment a is in front of b?
Visibility.segment_in_front_of = function(a, b, relativeTo)
// If the two segments have a common point (a frequent occurrence),
// then whichever is in closer is in front.
if (a.p1.x == b.p1.x and a.p1.y == b.p1.y) or
(a.p2.x == b.p1.x and a.p2.y == b.p1.y) or
(a.p1.x == b.p2.x and a.p1.y == b.p2.y) or
(a.p2.x == b.p2.x and a.p2.y == b.p2.y) then
return a.d < b.d
end if
// Otherwise, if A is in front, then both of its points will be on
// the same side of B as relativeTo is.
relOnLeft = self.leftOf(b, relativeTo)
return self.leftOf(b, a.p1) == relOnLeft and
self.leftOf(b, a.p2) == relOnLeft
end function
Visibility.sortEndpoints = function()
// sort endpoints first by angle, and in case they're equal, put begin before end
for e in self.endpoints
e.sortKey = e.angle + e.begin * 0.0001
end for
self.endpoints.sort "sortKey"
end function
// Run the algorithm, sweeping over all or part of the circle to find
// the visible area, represented as a set of triangles
Visibility.sweep = function(maxAngle = 999)
self.output = [] // output set of triangles
self.demo_intersectionsDetected = [];
self.sortEndpoints
open = []
beginAngle = 0.0
// At the beginning of the sweep we want to know which
// segments are active. The simplest way to do this is to make
// a pass collecting the segments, and make another pass to
// both collect and process them. However it would be more
// efficient to go through all the segments, figure out which
// ones intersect the initial sweep line, and then sort them.
text.row=24
for pass in [0,1]
//print char(13) + "PASS " + pass + ":" + char(13)
for p in self.endpoints
if pass == 1 and p.angle > maxAngle then
// Early exit for the visualization to show the sweep process
break;
end if
if open then current_old = open[0] else current_old = null
distToLine = mathUtil.distanceToLine(p.segment.p1, p.segment.p2, self.viewpoint)
if distToLine < 1 then continue // try skipping colinear walls
// ToDo: precompute that, along with the distance measure!
if p.begin then
// Insert into the right place in the list
i = 0
maxi = open.len
while i < maxi
if self.segment_in_front_of(p.segment, open[i], self.viewpoint) then
break
end if
i = i + 1
end while
//print "Inserting #" + p.segment.index + " at position " + i
open.insert i, p.segment
else
i = open.indexOf(p.segment)
//print "Removing " + p.segment.index + " from position " + i
if i != null then open.remove i
end if
//foo = []
//for o in open; foo.push o.index; end for
//print "open: " + foo + " beginAngle: " + (beginAngle*180/pi) + " p.angle: " + (p.angle*180/pi)
if open then current_new = open[0] else current_new = null
if current_old != current_new then
if pass == 1 then self.addTriangle beginAngle, p.angle, current_old
beginAngle = p.angle
//print "Updated beginAngle to " + (beginAngle*180/pi)
end if
end for
end for
self.cleanOutput // remove duplicate points, etc.
end function
Visibility.addTriangle = function(angle1, angle2, segment)
p1 = self.viewpoint
if segment != null then
//print "Adding #" + segment.index + " from " + (angle1*180/pi) + " to " + (angle2*180/pi)
// Stop the triangle at the intersecting segment
p3 = segment.p1
p4 = segment.p2
else
// Stop the triangle at a fixed distance; this probably is
// not what we want, but it never gets used in the demo
self.output.push Point.make(self.viewpoint.x + cos(angle1) * 500,
self.viewpoint.y + sin(angle1) * 500)
self.output.push Point.make(self.viewpoint.x + cos(angle2) * 500,
self.viewpoint.y + sin(angle2) * 500)
return
end if
p2 = Point.make(p1.x + cos(angle1), p1.y + sin(angle1))
point = lineIntersection(p3, p4, p1, p2)
// the "x == x" check here is a way to avoid pushing NaN points (from parallel lines)
if point.x == point.x then self.output.push point
if abs(angle2 - angle1) < 0.001 then return
p2 = Point.make(p1.x + cos(angle2), p1.y + sin(angle2))
point = lineIntersection(p3, p4, p1, p2)
if point.x == point.x then self.output.push point
end function
Visibility.cleanOutput = function()
i = self.output.len - 1
while i > 0
p = self.output[i]
p1 = self.output[i-1]
if p.x == p1.x and p.y == p1.y then
// if it's the same as the previous point (will generally be EXACTLY the same), remove it
self.output.remove i
else if i+2 < self.output.len then
// if it's very close to the point TWO above it, remove it and the one below
p1 = self.output[i+2]
if abs(p.x-p1.x) + abs(p.y-p1.y) < 0.0001 then
self.output.remove i+2
self.output.remove i+1
end if
end if
i = i - 1
end while
end function
Visibility.dumpPoints = function()
for i in self.output.indexes
print i + ". " + self.output[i].x + ", " + self.output[i].y
end for
end function
Visibility.draw = function(gfx)
gfx.clear
// draw visible region
if self.output then gfx.fillPoly self.output, "#CCCCFF44"
if true then
// draw segments in the environment
gfx.color = color.yellow
for seg in self.segments
gfx.line seg.p1.x, seg.p1.y, seg.p2.x, seg.p2.y
//p = interpolate(seg.p1, seg.p2, 0.5)
//gfx.print seg.index, p.x, p.y, color.orange, "small"
end for
end if
if false then
// draw endpoints
gfx.color = color.orange
for i in self.endpoints.indexes
e = self.endpoints[i]
gfx.fillEllipse e.x-4, e.y-4, 8, 8
gfx.print i, e.x+4, e.y+4 - 10*(i%2), "#444444", "small"
end for
end if
// draw the light location
gfx.fillEllipse self.viewpoint.x-10, self.viewpoint.y-10, 20, 20, color.yellow
end function
lineIntersection = function(p1, p2, p3, p4)
// From http://paulbourke.net/geometry/lineline2d/
// Note that it will return NaN, NaN if the lines are colinear.
s = ((p4.x - p3.x) * (p1.y - p3.y) - (p4.y - p3.y) * (p1.x - p3.x)) /
((p4.y - p3.y) * (p2.x - p1.x) - (p4.x - p3.x) * (p2.y - p1.y))
return Point.make(p1.x + s * (p2.x - p1.x), p1.y + s * (p2.y - p1.y))
end function
// Return p*(1-f) + q*f
interpolate = function(p, q, f)
return Point.make(p.x*(1-f) + q.x*f, p.y*(1-f) + q.y*f)
end function
if locals == globals then
// Let's do a test!
clear
display(2).mode = displayMode.pixel
g = display(2)
g.clear
y = 560
gprint = function(s)
g.print s, 610, y, color.orange, "small"
outer.y = y - 15
end function
g.print "2D Visibility Demo", 650, y+40, color.orange
gprint "This program calculates the area"
gprint "visible from any point, taking into"
gprint "account obstacles defined as"
gprint "arbitrary line segments."
gprint
gprint "Click and drag to move the light."
gprint "Press Esc to exit."
vis = Visibility.make
vis.loadMap 600, 10
vis.addBlock 150,360, 60
vis.addBlock 400,150, 60,80
vis.addSegments [[200,500],[300,500],[300,400],[400,400],[500,500]]
vis.addSegments [[140,150], [100,150], [100,100], [200,100], [200,150], [160,150]]
vis.setViewpoint 300, 300
vis.sweep
vis.draw gfx
counts = []
clamp = function(x, min, max)
if x < min then return min
if x > max then return max
return x
end function
while not key.pressed("escape")
newx = clamp(mouse.x, 11, 589)
newy = clamp(mouse.y, 11, 589)
if mouse.button and (newx != vis.viewpoint.x or newy != vis.viewpoint.y) then
// change the viewpoint, and do a new sweep
vis.setViewpoint newx, newy
vis.sweep
// yield (to get a frame break), then draw the new vis area
yield
vis.draw gfx
else
yield
end if
end while
key.clear
end if